Introduction To Linear Algebra

Introduction to Linear Algebra is a course by Gilbert Strang for MIT

When we look at equations, we have a few different perspectives

3x + 2y = 4
-x + 2y = 3

We can visualise it as the following forms

Matrix Form

$$\left[\begin{array}{cc}3& 2\\ -1& 2\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{c}4\\ 3\end{array}\right]$$

Row Form

This is when we try to rewrite it in the original $y=mx+c$ form that we learnt in school

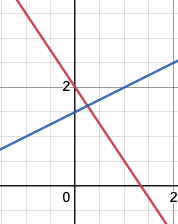
Column View

We can also visualise it as a linear combination of vectors

$$x\left[\begin{array}{c}3\\ -1\end{array}\right]+y\left[\begin{array}{c}2\\ 2\end{array}\right]=\left[\begin{array}{c}4\\ 3\end{array}\right]$$

All three are equally valid ways of visualising the problem but when we get to higher dimensions, the row and column views start to be a bit more limited in their usage since it gets difficult to visualise.

If all vectors are within the same plane, then we cannot discover a unique vector that is an answer to the solution